Teknologi / 7 minutter / 22. januar 2023

Anta bias. Alltid

Et maskinlæringssystem blir aldri helt rettferdig. I alle fall ikke mer rettferdig en de data modellen er trent på. Og datasettene vi benytter foreslår som hovedregel at vi diskriminerer.

Nora Gjøen-Gjøsæter

Data scientist

De data vi benytter for å trene modeller kan inneholde informasjon som kan oppfattes som urettferdig eller diskriminerende. Det skyldes ikke nødvendigvis feil i datasettet. Det kan for eksempel skyldes sammenhenger vi ikke har tatt høyde for, eller visse grupper som er underrepresentert.

Det er mulig å fjerne, eller i minste fall dempe, bias fra en maskinlæringsmodell. Men det er ikke nødvendigvis riktig, enkelt eller ønskelig.

For å forstå utfordringene med å fjerne bias fra en modell, skal vi ta for oss et ganske enkelt, men virkelighetsnært scenario. Vi i Kantega har faktisk bygget en modell med omtrent akkurat samme formål for SpareBank 1 Kreditt.

Et eksempel — Lånesøknader

I dette eksempelet ønsker vi å finne sannsynligheten for at en kunde kommer til å misligholde sine låneforpliktelser. Vi benytter et syntetisk datasett, men utfordringene vi må løse er høyst realistiske.

Du kan kjøre gjennom eksempelet selv her.

Datasettet

La oss innta rollen som maskinlæringsteam i Rettferdig Bank. Vi skal bygge vår egen maskinlæringsmodell for å vurdere om vi vil innvilge lån til kunder. Vi vil bare innvilge lån til kunder vi tror vil betale tilbake på normert tid.

Vi antar at lånebeløpet er helt likt for alle lånesøknader, og tar utgangspunkt i et historisk datasett, som vi ser et utvalg fra under.

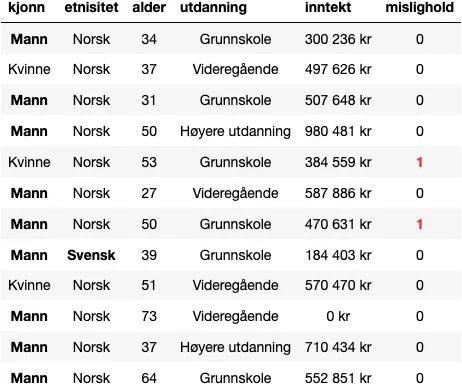
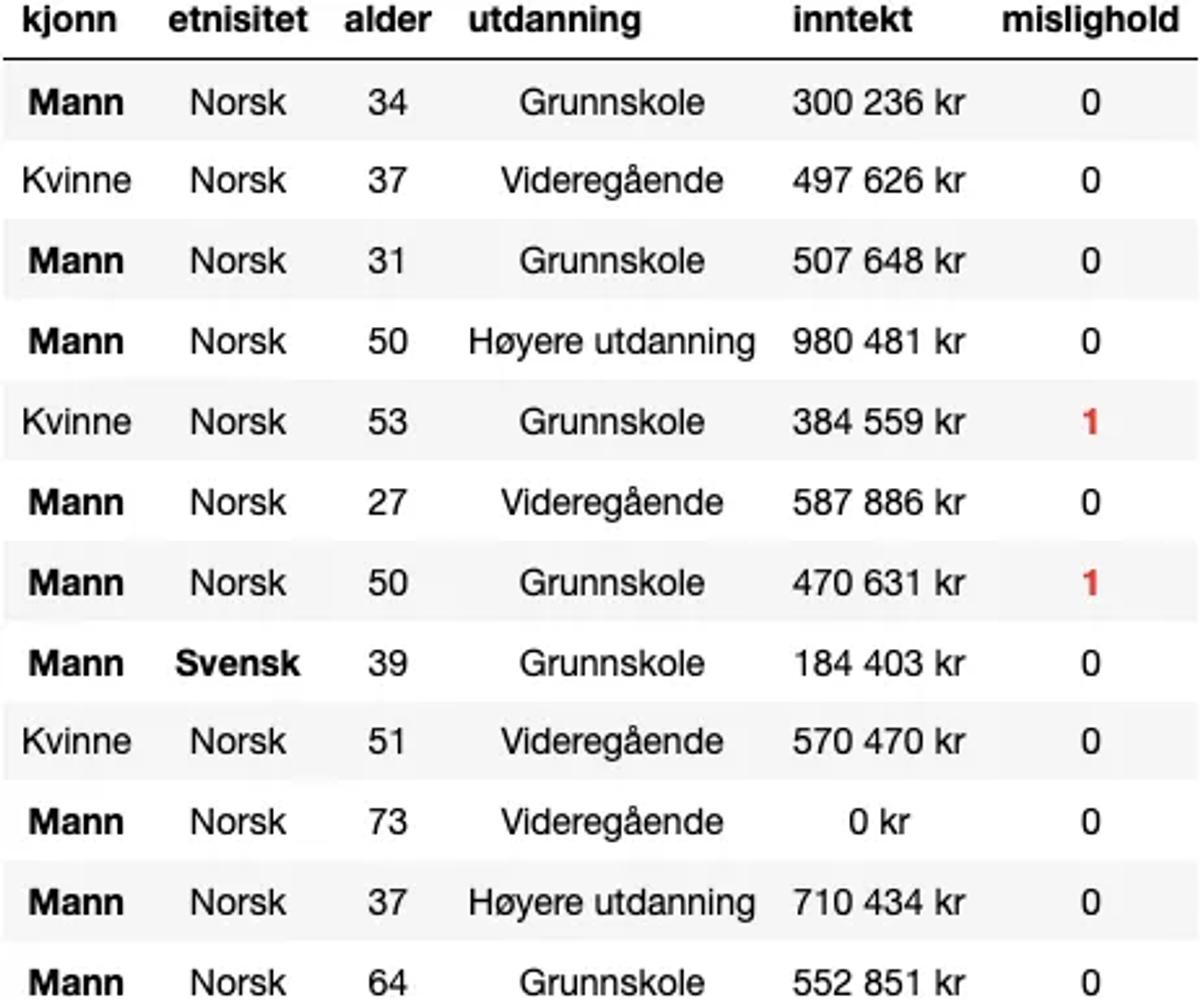
I vårt datasett har vi følgende forklaringsvariabler: Kjønn, etnisitet, alder, utdanning og inntekt. Utfallsvariabelen, mislighold, beskriver hvorvidt vedkommende har misligholdt sine låneforpliktelser. Vi ønsker å gi lån til kunder som ikke vil misligholde sine lån, altså rader der mislighold = 0.

Som Rettferdig Bank ønsker vi verken å diskriminere på grunnlag av kjønn eller etnisitet, så vi begynner rett og slett med å fjerne disse variablene, og sitter da igjen med følgende utgangspunkt:

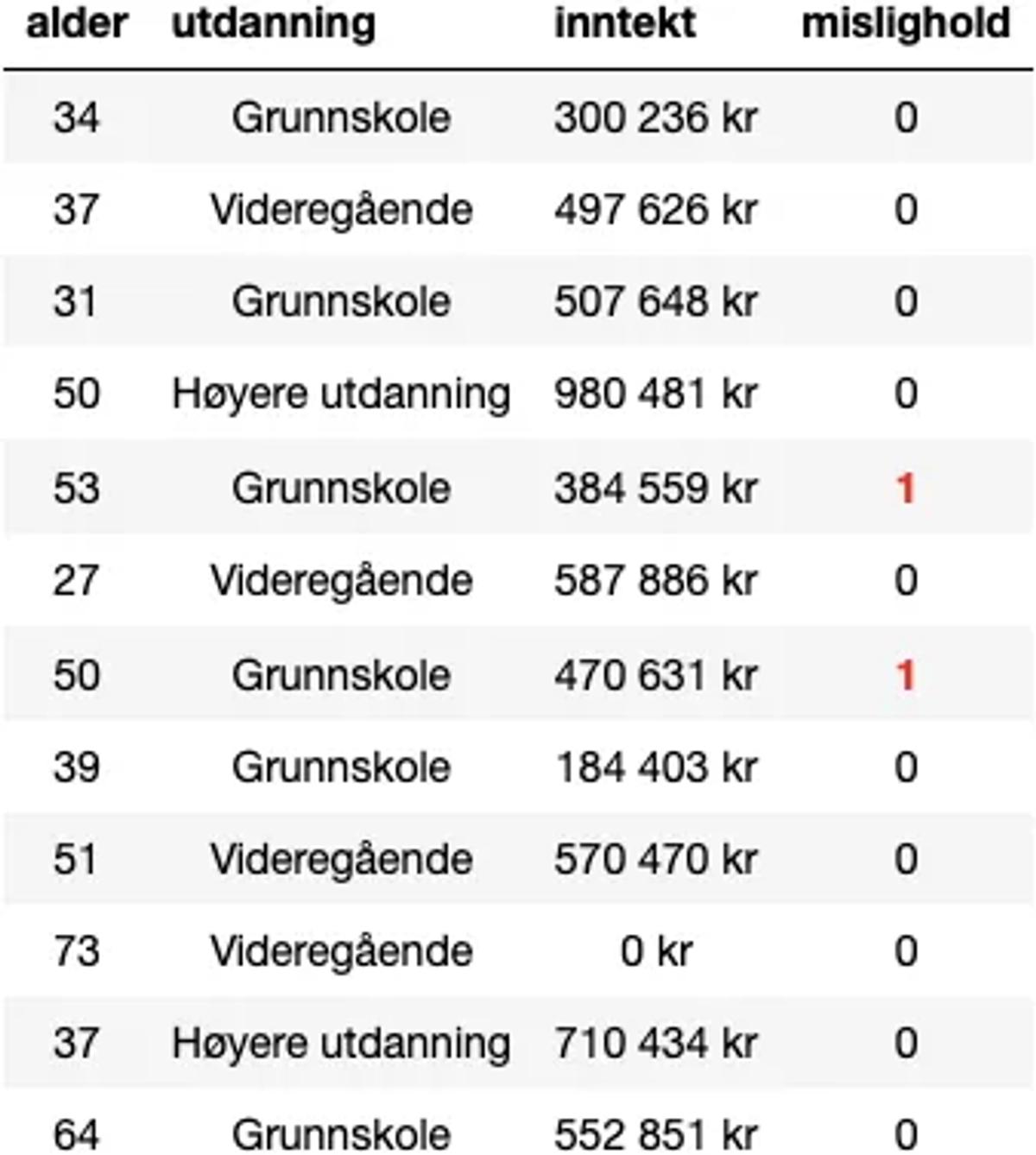
Vi har bestemt oss for at det er greit å bruke både alder, utdanning og inntekt for å bestemme hvem som bør for lån. Nå er vi vel ganske safe?

Naiv modellering

Vi er superivrig — endelig skal vi i gang med maskinlæring for lånevurderinger. Vi hopper rett i trening av et nevralt nettverk som skal si noe om sannsynligheten for mislighold.

Nevrale nettverk er fleksible matematiske skapninger som kan plukke opp komplekse sammenhenger i data. Også er det ganske kult å kunne si at lånesøknadsvurderingen vår er basert på dyp læring.

Vi får endelig ta i bruk maskinlæring for å behandle lånesøknader! Bildet er generert med Stable Diffusion v1.4. Anta bias fra modellen i seg selv, og prompten som er brukt for å generere akkurat dette bildet

Vi trener nettverket på et ganske stort datasett, og evaluerer på et separat testdatasett. Og vi oppnår ganske gode resultater.

I testdatasettet vårt, predikerer vi korrekt (mislighold eller ikke mislighold) på 71 % av alle kunder. Ikke verst, med så få forklaringsvariabler. Og en god del bedre enn gjetning.

Toppledelsen i Rettferdig Bank er overbevist, og skikkelig glad for å kunne si at vi er i gang med AI. Innen en uke er modellen satt i drift.

Hurra!

Vi har et problem

Etter at modellen har vært i drift et par uker kommer fru Skeptismo fra Complianceavdelingen på besøk i modelleringskroken vår. Hun har oppdaget at vi innvilger en langt større andel av menns lånesøknader enn kvinners. Vi gir også mindre lån til svensker. Fru Skeptismo vil gjerne ha en forklaring.

Vi bestemmer oss for å undersøke nærmere. Vi ser på kundene som i testdatasettet, og undersøker hvor ofte kunder i hver gruppe blir predikert til å misligholde sine forpliktelser.

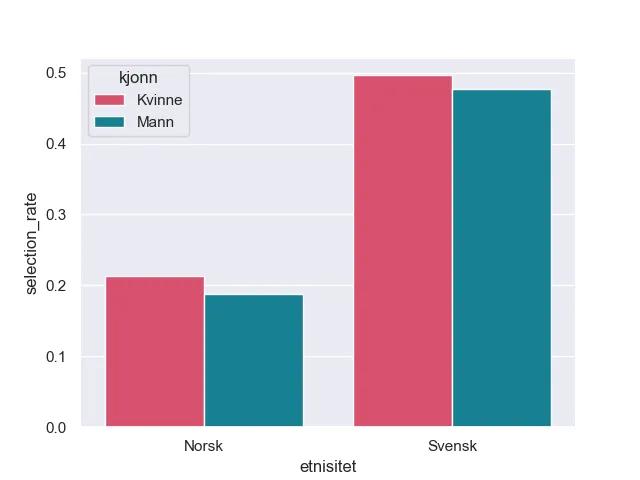
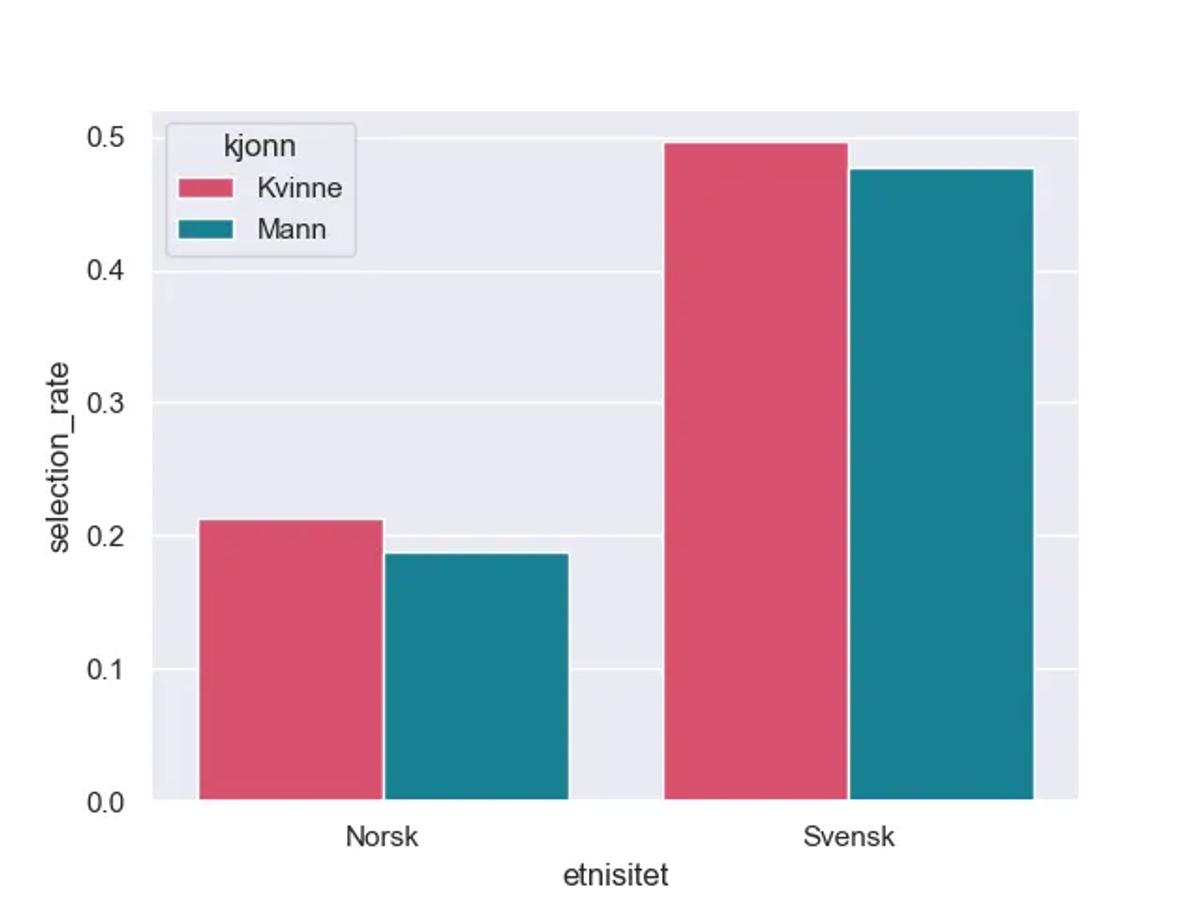
Seleksjon her betyr at at kundene ikke får innvilget lån, fordi de predikeres til å misligholde. Norske menn får oftere lån enn både kvinner og svensker

Whops. Fru Skeptismo har rett. Svensker og kvinner blir i større grad nektet lån. Aller verst er det faktisk for svenske menn.

Hva har egentlig skjedd her? Vi brukte jo ikke noe data om verken kjønn eller etnisitet da vi trente modellent?

Data er alt

Forklaringen ligger i datasettet som er brukt for å trene modellen vår. For selv om vi ikke har benyttet kjønn og etnisitet direkte, er det en sammenheng mellom disse sensitive variablene og forklaringsvariablene vi faktisk har tatt i bruk.

Greit nok, kunne vi sagt. Da er det noe sammenhenger der, men vi har ikke modellert inn noe eksplisitt, så det er vanskelig å bevise at vi har gjort dette intensjonelt. Og det må jo være greit å bruke inntekt, alder og utdanning for å vurdere hvem som skal få lån?

Men vi tar ikke denne enkle veien. Vi, vi er Rettferdig Bank— og bestemmer oss for å grave dypere.

Hvorfor ber modellen oss diskriminere?

Vi burde selvfølgelig gjort en skikkelig eksplorativ dataanalyse før vi satte i gang med modelleringen. Men det er mye gøyere å bygge nevrale nettverk enn å se på korrelasjonsmatriser.

Når det nå viser seg at modellen i stor grad nekter å gi lån til kvinner og svensker, er det heldigvis åpenbart at vi må forstå data bedre.

Vi begynner med å titte på de data vi brukte for å trene modellen.

Her viser det seg blant annet at menn tjener mer enn kvinner, og at nordmenn tjener mer enn svensker.

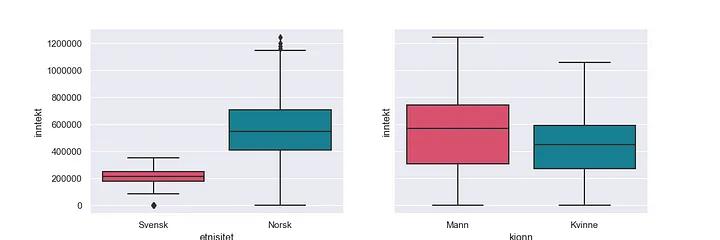
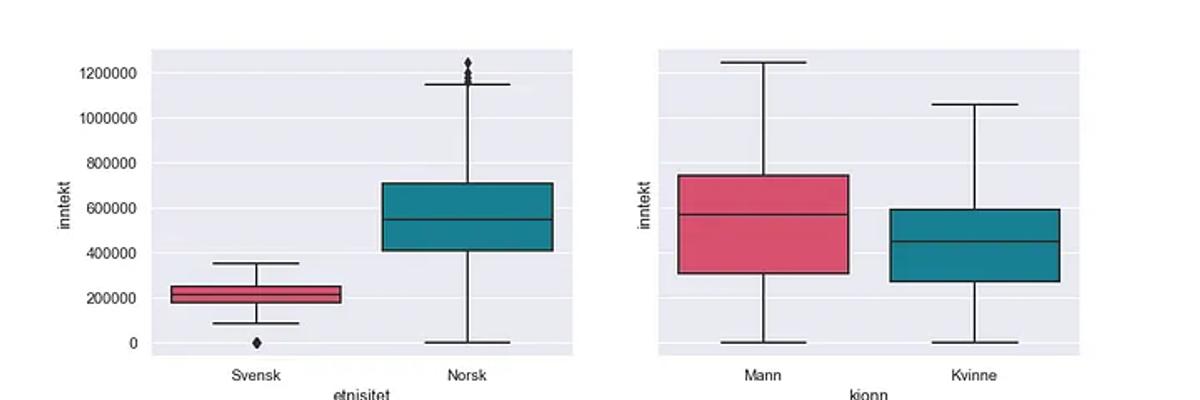
Boksplott for inntekt viser at svensker tjener mindre enn nordmenn, og at menn tjener mer enn kvinner

Siden modellen allerede er i drift, må vi selvfølgelig også granske denne. Vi ser på (gjennomsnittlig) avhengighet til forklaringsvariablene vi har tatt i bruk.

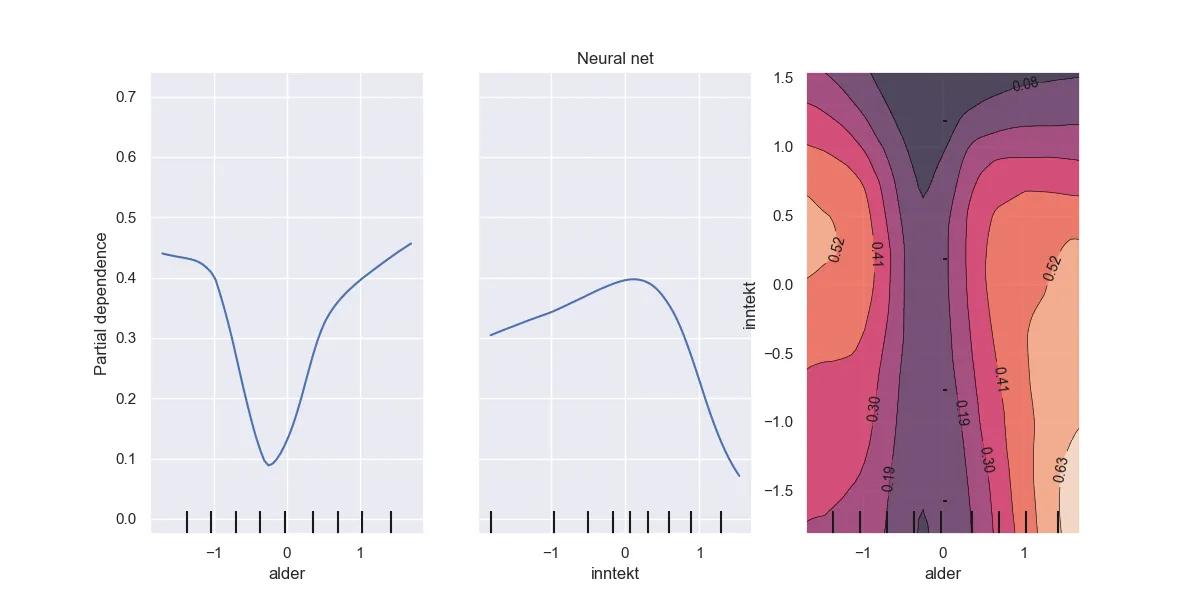
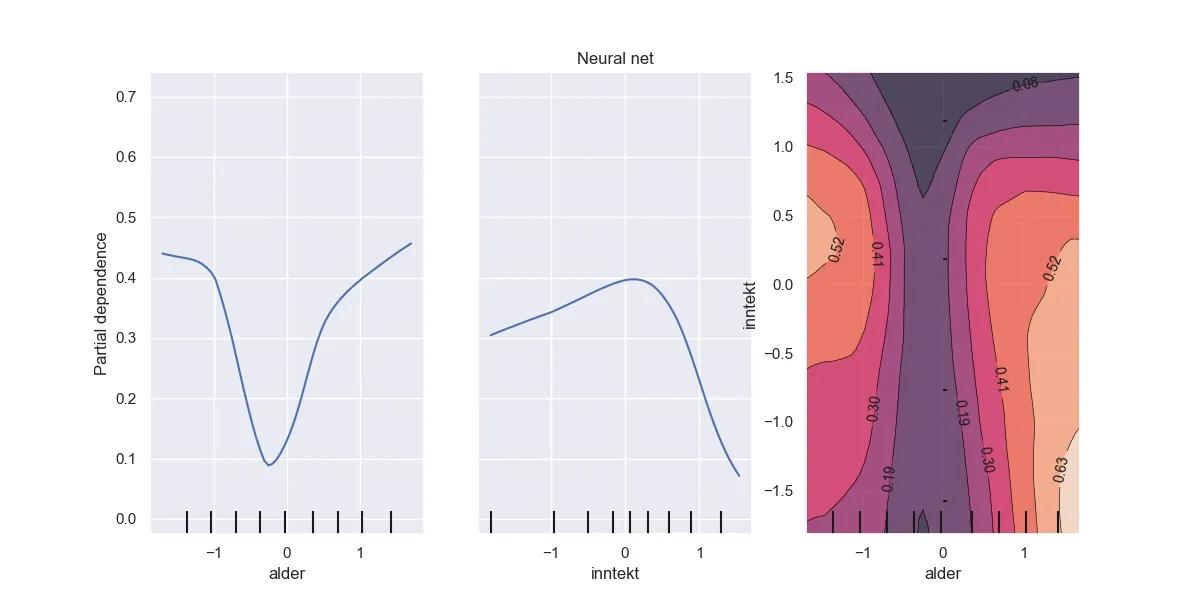
Partielle avhengighetsplott. Generelt gir høyere inntekt lavere estimert sannsynlighet for mislighold. Det samme gjør det å være i midten av livet. Merk at forklaringsvariablene er skalert.

Vi ser blant annet at høyere utdanning og inntekt, gir lavere estimert sannsynlighet for mislighold.

Dette stemmer kanskje generelt. Men vi vet ikke om dette stemmer i like stor grad for begge kjønn, eller svensker, fordi vi har ekskludert både kjønn og etnisitet fra modelleringen. Vi kan dermed ikke justere for skjevheter.

Svensker er dessuten kraftig underrepresentert.

Stemningen er ikke like god når vi finner ut at modellen gjør det vanskelig for kvinner og svensker å få lån. Bildet over er modifisert med Stable Diffusion. Anta bias.

I tillegg finner vi et stort problem med selve datasettet. Alle svensker er nemlig registrert med “Grunnskole” som utdanning. Det kan åpenbart ikke være riktig, og skyldes sannsynligvis måten data er hentet og definert på. Kanskje har det ikke vært mulig å hente data fra svenske utdanningsinstitusjoner.

Vi kan nå forklare en del av mekanismene som gjør at vi ender opp med å predikere at både kvinner og svensker i mindre grad vil oppfylle sine betalingsforpliktelser.

Så hva bør vi gjøre? Må vi forkaste modellen? Er det greit at vi har det sånn? Kan vi gjøre noe med dette, uten å ødelegge forklaringskraften i modellen?

Hva er en rettferdig modell?

Før vi eventuelt gjør grep, bør vi stille oss selv det virkelig store spørsmålet: Hva er egentlig rettferdig når man trener en maskinlæringsmodell?

Dette er, dessverre, fullstendig avhengig av kontekst.

I noen tilfeller er det kanskje greit å diskriminere, hvis data sier at enkelte grupper bør vurderes ulikt. For eksempel priser vi bilforsikring etter alder, fordi unge sjåfører krasjer oftere. Likevel godtar vi ikke at unge menn må betale mer enn unge kvinner, selv om historiske data sier at risikoen er langt høyere i denne gruppen.

I noen tilfeller er det verste for en spesiell gruppe at modellene er unøyaktige. For eksempel kan en smarthøyttaler tolke bergensere dårligere enn østlendinger, og dermed gi mindre verdi for de som skarrer. Her vil vi helst eliminere bias for å sikre like god opplevelse uansett dialekt.

Det et mange måter å definere ‘rettferdighet på’. Bildet er generert med Stable diffusion.

I andre tilfeller, som i vårt lånesøknadseksempel, er det å bli selektert enten en fordel eller en ulempe.

Det er flere måter å vurdere rettferdighet på i en kontekst der det å bli valgt eller ikke valgt kan oppleves urettferdig:

Demografisk paritet: Seleksjonsraten skal være lik på tvers av alle gruppene
Sann-positiv paritet: Sann-positiv-raten skal være lik på tvers av alle gruppene.
Utlignet odds: Både sann-positiv-raten og falsk-positiv-raten skal være lik på tvers av alle grupper.

Demografisk paritet er kanskje lettest å forstå — vi skal velge like stor andel fra hver gruppe, uansett hvordan disse andelene ser ut i treningsdata.

Sann positiv-rate-rate betyr hvor stor andel av de som predikeres som positiv som faktisk er det. I vårt eksempel vil det ved sann-positiv-paritet være like høy sannsynlighet for at du faktisk misligholder lånet, gitt at det har blitt predikert at du vil gjøre det, uansett hvilken gruppe du er i.

Tilsvarende er falsk-positiv-rate hvor stor andel av de som predikeres å være positiv, som ikke viser seg å være det. I vårt tilfelle ville det betydd at det er like stor andel av de vi nekter lån, som egentlig ville ha oppfylt sine betalingsforpliktelser, på tvers av alle grupper. Vi kan gjerne kalle dette ‘falsk alarm’.

En må vurdere i hvert tilfelle hvilken rettferdighetsmetrikk en ønsker å oppnå, og hvorfor det er riktig.

Skadebegrensing i låneeksempelet

La oss hoppe tilbake til vårt eksempel, og se hvordan modellen vår ser ut etter rettferdighetsmetrikkene vi nettopp har gått gjennom.

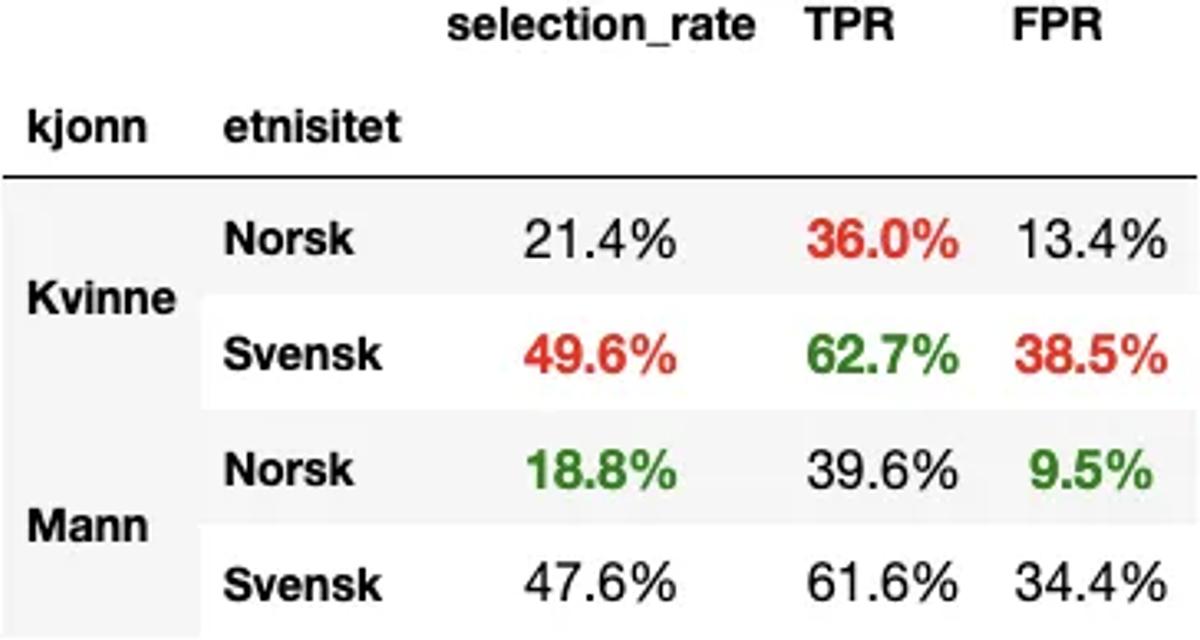
TPR = True Positive Rate (Sann-positiv-rate). FPR = False Positive Rate (‘Falsk alarm’-rate)

Som vi allerede har sett er seleksjonsraten til fordel for norske menn, og til ulempe for kvinner og svensker. Men ser vi på sann-positiv-raten (TPR) og falsk-alarm-raten(FPR), blir bildet straks mer komplekst.

Svenske kvinner for eksempel, har høyest seleksjonsrate, men likevel også høyest sann-positiv-rate. Altså er det størst sannsynlighet for at et individ i denne gruppen faktisk misligholder lånet, gitt at hun ble predikert til å gjøre det. Mens det dessverre også er denne gruppen som har høyest falsk-alarm-rate, altså sannsynlighet for å bli nektet lån selv om man ville ha betalt.

La oss nå si at vi ikke sikter oss inn på å jevne ut seleksjonsraten (demografisk paritet). Vi godtar at utdanning og inntekt henger sammen med kjønn og etnisitet, og at denne sammenhengen gjør at vi kommer til å nekte noen grupper lån i større grad.

Men vi ønsker å sikte mot utlignet odds, spesielt fordi vi er opptatt av at det skal være relativt lik falsk-alarm-rate i alle gruppene. Vi ønsker altså ikke å feilaktig nekte lån i større grad i noen av gruppene.

Biasdemping i praksis

For å forsøke å gjøre modellen mer rettferdig tar vi i bruk en optimaliseringsalgoritme for å balansere opprettholdt nøyaktighet i modellen, og grep for å oppnå utlignet odds. Det er ikke alltid mulig å finne et perfekt punkt som sikrer både lik FPR og TPR, men en kommer langt nærmere enn vi var under det naive modelleringsregimet.

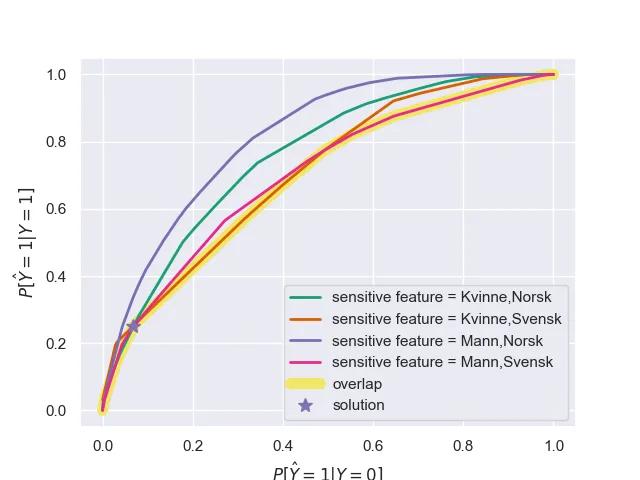
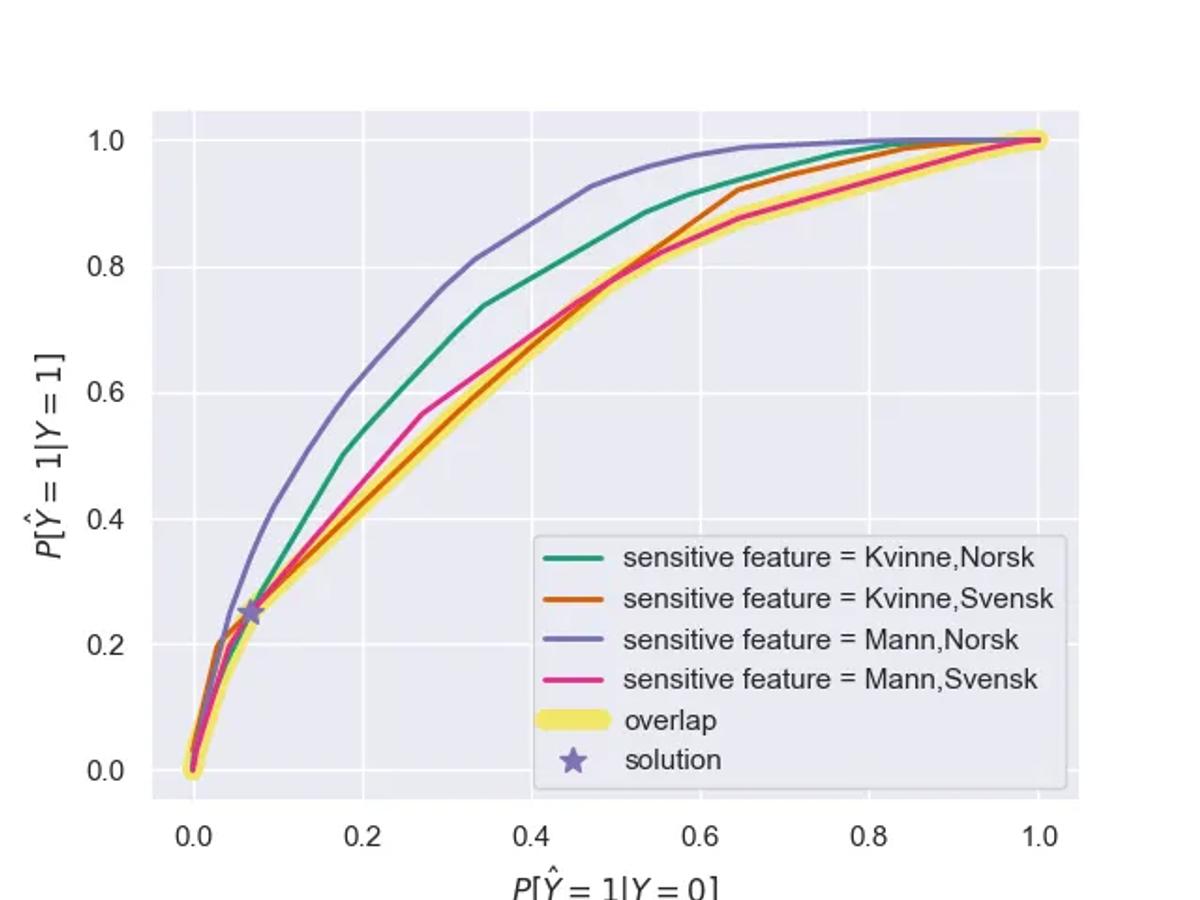
ThresholdOptimizereren finner punktet som sikrer lav ulikhet i både falsk-alarm og sann-positiv-raten i alle grupper

Etter at vi justerer modellen vår gjennom denne algoritmen ender vi opp med følgende ‘rettferdighetstabell’:

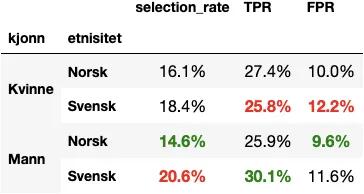
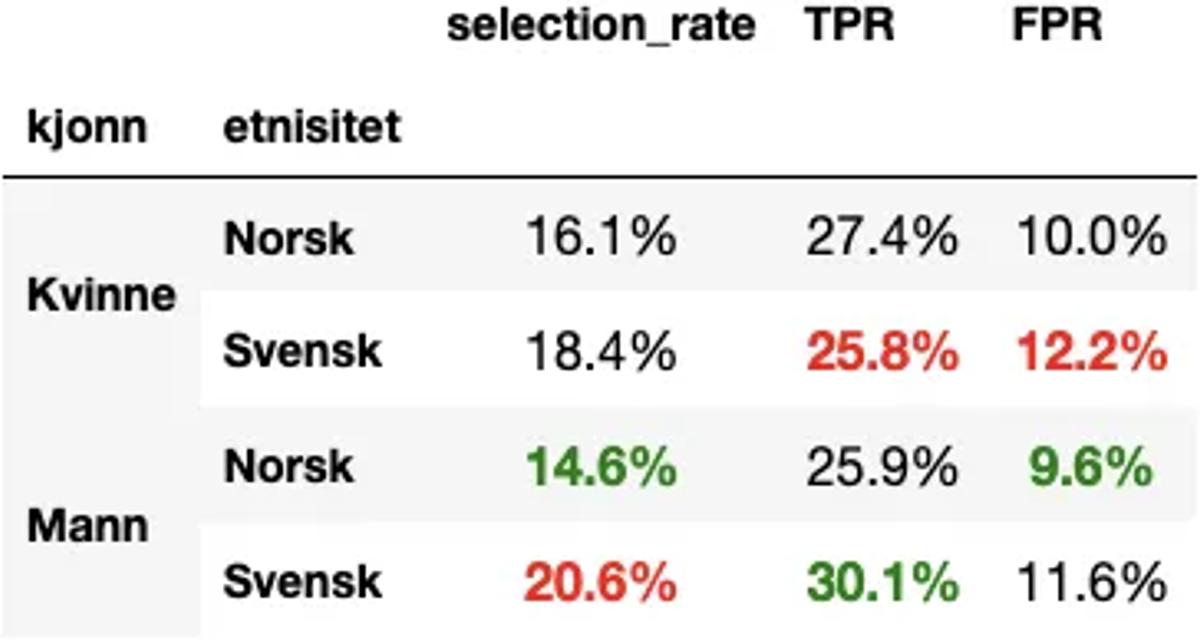
Vi ser at falsk-alarm-raten og sann-positiv-raten nå er mye mer lik på tvers av gruppene. Det er fortsatt forskjell i seleksjonsraten, men det har vi altså godtatt. Så kan en være uenig i om det er greit eller ikke.

Selv om denne tabellen ser bedre ut, er ikke alt forbedret. Treffsikkerheten vår har falt fra over 71 % til under 68 %. Det er ikke gitt at dette ville ha et slikt utslag, men en kan altså risikere å miste noe nøyaktighet i det en tilstreber for eksempel utlignet odds.

En urettferdig verden

Noen vil kanskje legge merke til at maskinlæringen i seg selv ikke kan ta hele skylden for bias i dette eksempelet. Faktisk ville en enkel regel som ‘de med inntekt over X får lån’ også føre til at en mindre andel kvinner og svensker fikk lån enn norske menn.

Skulle et menneske gjort hele lånesøknadsvurderingen på egenhånd, uten regler, ville en også måtte anta en hel del bias.

Men det er heldigvis en del grep vi som bygger modeller kan ta, for å begrense urettferdighet ved maskinlæringsmodellering.

Første steg er å være klar over at modellene våre vil finne disse ‘urettferdige’ mønstrene i data, og de vil da også bruke disse for å gjøre bedre prediksjoner.

Har vi først erkjent at modellene våre sannsynligvis inneholder bias — bør vi etter beste evne også avdekke, demonstrere og eventuelt også dempe virkningen av slik bias.

Helt i mål kommer vi sannsynligvis ikke — men vi kan prøve å gjøre modellene våre, og med det også verden — litt mer rettferdig. Etter en eller annen tolkning av rettferdighet. Som sikkert også er biased.