Avanserte maskinlærekonsepter: Aktiv læring

Del 2: Aktiv Læring

I forrige artikkel utforsket vi Autoenkodere, en arkitektur for nevrale nettverk som kan brukes til å løse forskjellige unsupervised learning- relaterte problemer. I denne artikkelen skal vi i se på en strategi for å trene supervised learning-modeller.

Hvorfor aktiv læring?

Når man skal trene en supervised learning-modell til f.eks å klassifisere bilder, trenger man gjerne et stort datasett med labeled samples. Jobben med å gå gjennom alle dataene og merke de med korrekt label, blir som oftest gjort av mennesker og er svært tid- og kostnadskrevende. (F.eks et datasett bestående av flere millioner bilder).

Aktiv læring er et alternativ til den “vanlige” måten å trene supervised learning-modeller på, i tilfeller der man sitter på store mengder data som ikke har blitt lablet enda.

Fordeler med aktiv læring er blant annet:

• Kun merke samples som modellen lærer mye fra
• Spare tid og penger ved å redusere tiden brukt på å merke samples

Hva er aktiv læring?

Aktiv læring er en strategi der vi i motsetning til å merke hele datasettet før trening, iterativt merker samples i datasettet under trening av modellen.

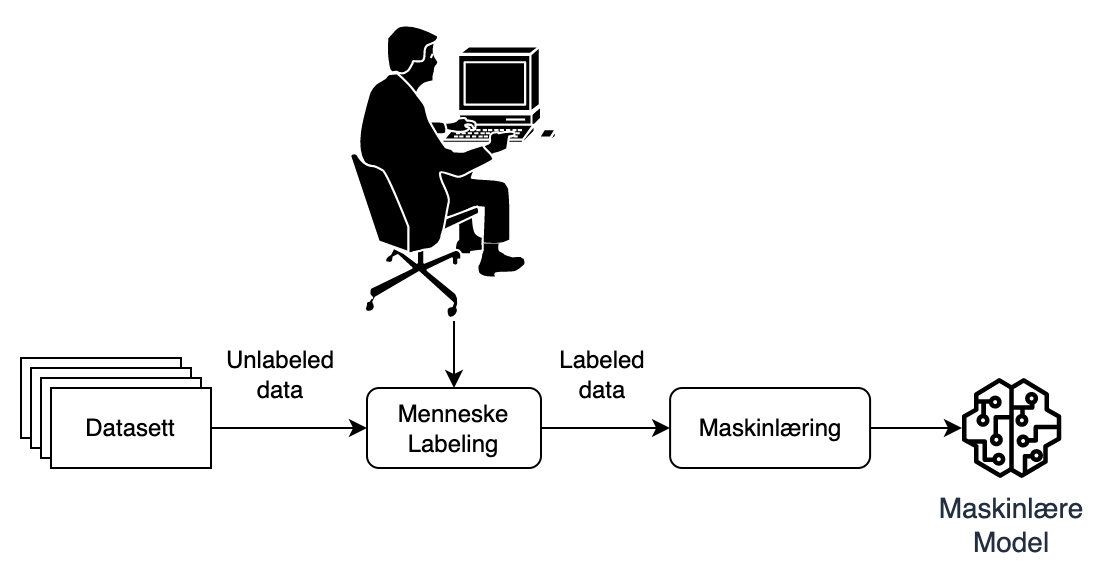
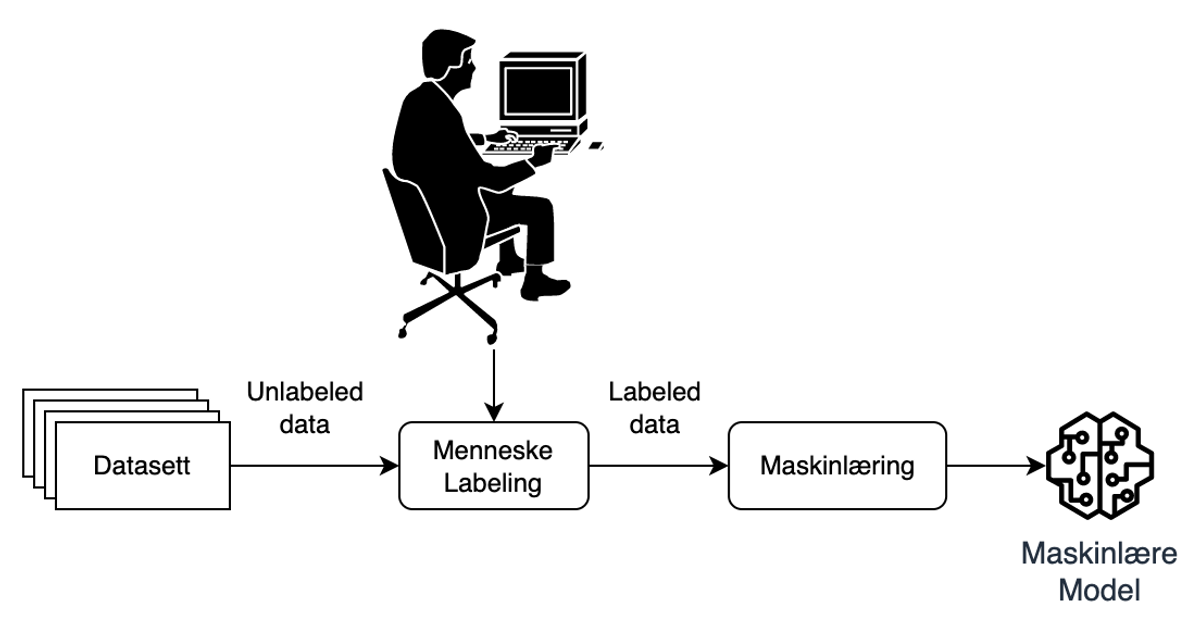
Figur 1: Typisk trening av supervised learning model

Figur 1: Typisk trening av supervised learning model

I Figur 1 kan man se en enkel illustrasjon av hvordan en typisk supervised learning-modell blir trent. Først må alle samples i datasettet merkes av mennesker, deretter brukes datasettet til å trene en maskinlæremodell.

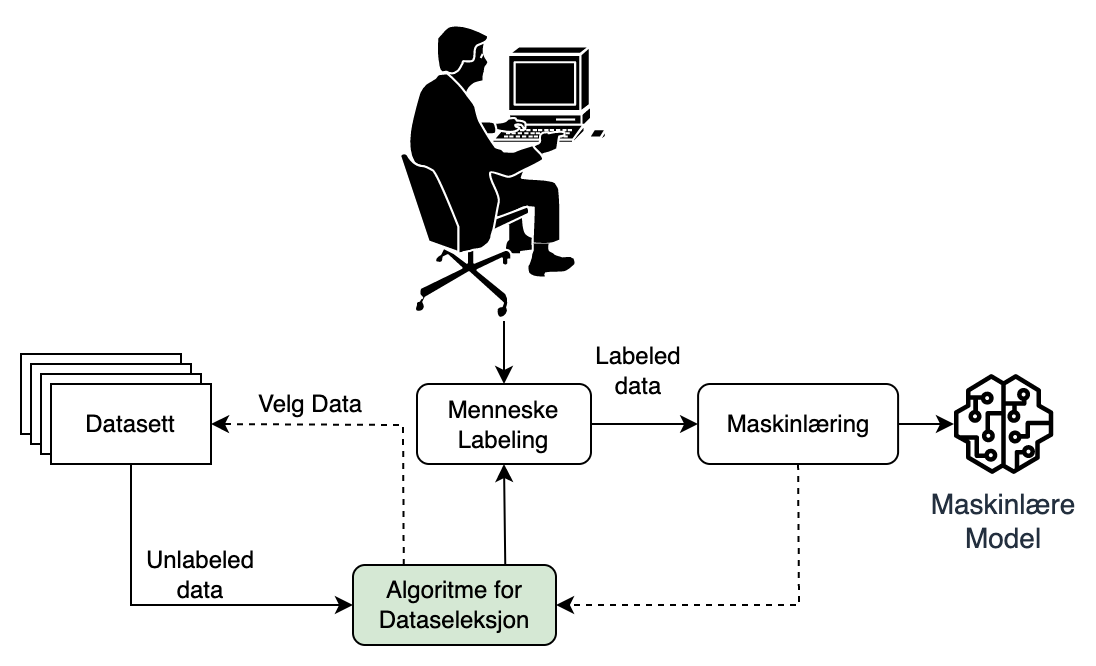
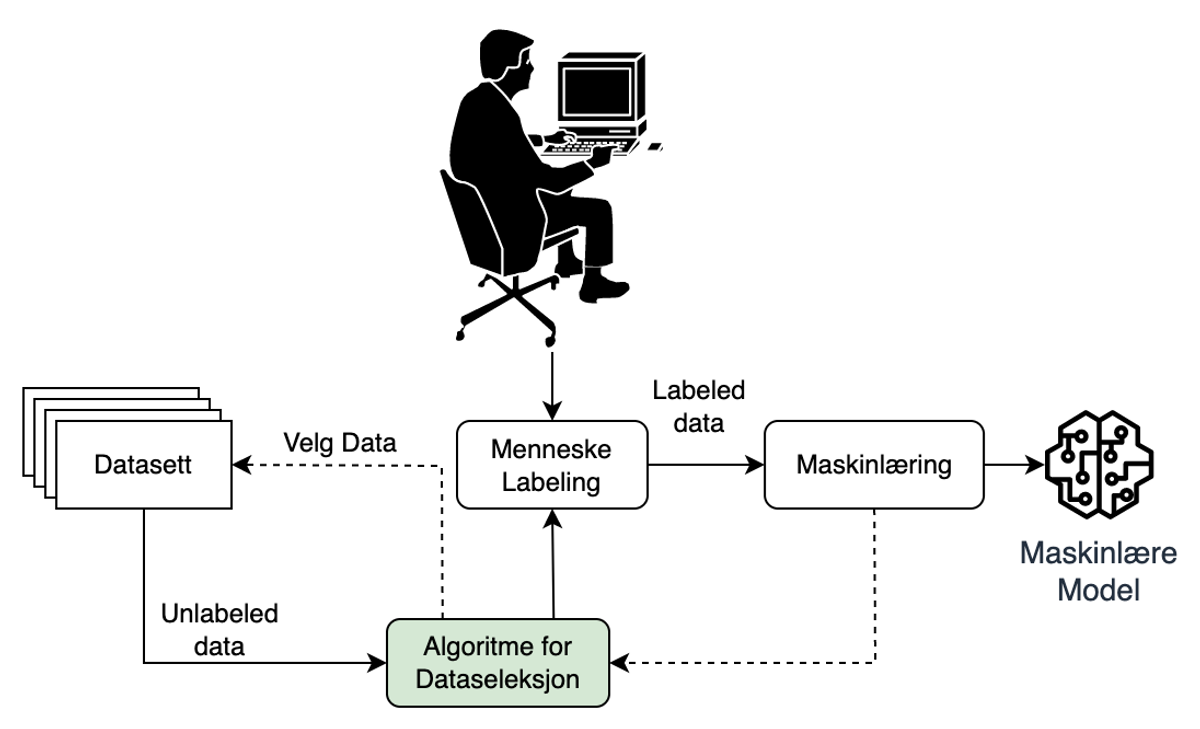
Figur 2: Trening gjennom aktiv læring

Figur 2: Trening gjennom aktiv læring

I Figur 2 kan vi se hvordan en modell blir trent under aktiv læring. I motsetning til standard fremgangsmåte (Figur 1), kan vi se at vi nå har lagt til et nytt steg; “Algoritme for Dataseleksjon”. I stedet for at hele datasettet blir merket før treningen starter, skjer dette nå iterativt i løpet av treningsprosessen.

Med andre ord kommer styrken til denne strategien i form av hvordan dataseleksjonsalgoritmen prioriterer samples som menneskene skal merke.

I neste avsnitt skal vi leke oss med MNIST datasettet[1] og gjennomføre et eksperiment som forhåpentligvis kan vise hvorfor det er lurt å bruke aktiv læring!

Hvordan fungerer aktiv læring?

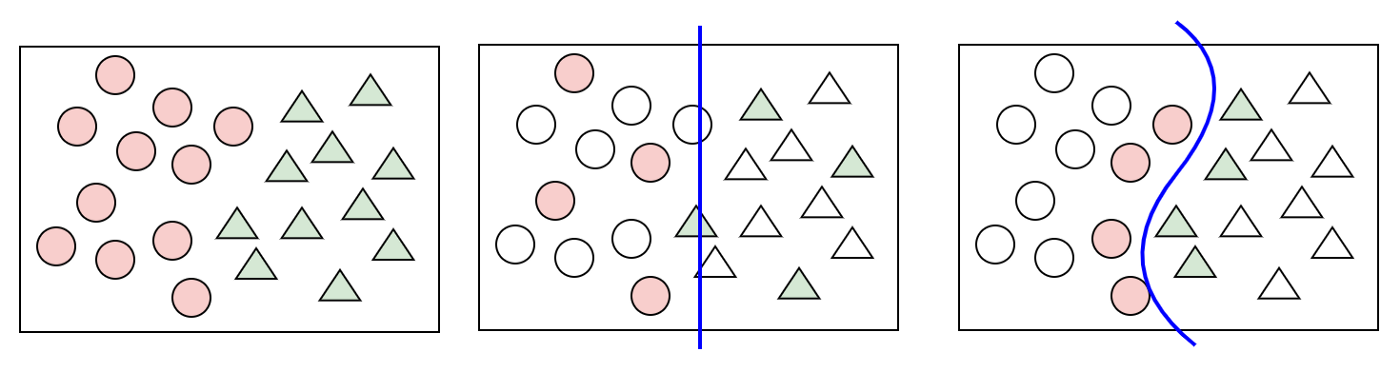
Figur 3: Datasett med 2 klasser (t.v), classifier på random utvalg (midten) og classifier på samples valgt gjennom aktiv læring (t.h)

Figur 3: Datasett med 2 klasser (t.v), classifier på random utvalg (midten) og classifier på samples valgt gjennom aktiv læring (t.h)

I figuren over kan vi se en enkel illustrasjon av hvordan aktiv læring fungerer. Til venstre ser vi et datasett bestående av 2 klasser der dataene i datasettet består av 2 dimensjoner. I det midterste plottet har vi valgt et random antall samples fra datasettet og trent en modell til å skille de 2 klassene fra hverandre. Til slutt, i plottet til høyre, har vi brukt aktiv læring. Her kan vi se at de samplene som nå er valgt er de som ligner mest på samples fra den andre klassen, og som gjerne er vanskelig for modellen å skille fra hverandre. Antagelsen er at hvis modellen klarer å skille disse fra hverandre, klarer den også å skille de resterende samplene fra hverandre.

Illustrasjonen i Figur 3 er fin for å få et inntrykk av hvordan aktiv læring fungerer, men som vi alle vet så er ekte datasett som oftest ikke så enkle. De består gjerne av flere enn bare 2 klasser og dataene har gjerne mange dimensjoner. Målet for resten av artikkelen vil være å gjennomføre et eksperiment på et multidimensjonelt datasett med mange klasser, for så å visualisere eksperimentet i plot som ligner på dem over.

MNIST

I eksperimentet vårt skal vi bruke MNIST datasettet. Dette er et ferdig merket datasett bestående av 70 000 28x28 pixler store bilder av håndskrevne tall. Vi kommer til å late som bildene ikke har blitt merket enda, og bruker i stedet kode til å “simulere” markeringsprosessen.

PCA og t-SNE-visualisering

Det første vi støter på når vi jobber med multidimensjonelle datasett med mange klasser, er at vi ikke lenger kan plotte dataene direkte i et 2D-scatterplot. Heldigvis finnes det metoder som kan hjelpe oss med dette.

I denne artikkelen skal vi bruke metodene Principal Component Analysis (PCA) [2] og t-SNE [3] for å hjelpe oss med å visualisere resultatene fra eksperimentet vårt. Vi vil ikke gå i detalj på hvordan disse fungerer, men heller gi en kort oppsummering. PCA er en metode for å redusere antallet dimensjoner i dataene uten å miste for mye variasjon i datasettet. t-SNE brukes til å redusere høyere dimensjonelle data til 2D-space, slik at de kan visualiseres i et 2D scatterplot.

Figur 4: Scatterplot av MNIST vha. PCA og t-SNE

Figur 4: Scatterplot av MNIST vha. PCA og t-SNE

I figuren over kan vi se et scatterplot av MNIST datasettet, etter å ha brukt PCA og t-SNE for å redusere antallet dimensjoner. I figuren tilsvarer hver “prikk” en sample og vi kan se at datasettet har blitt fordelt i ti, roughly, distinkte grupperinger. Dette stemmer godt overens med hva vi forventer med tanke på at datasettet består av 10 klasser, en klasse for hver av tallene fra 0 til 9.

Med en metode for å visualisere dataene våre kan vi endelig gyve løs på selve eksperimentet vårt!

Aktiv læring

Målet i resten av artikkelen vil være å trene 2 classifiers på MNIST datasettet. En der vi iterativt velger tilfeldige samples fra MNIST og trener modellen. Og en annen der vi velger samples på en “smartere” måte, der vi prioriterer samples som vi tror modellen kan lære mest mulig av.

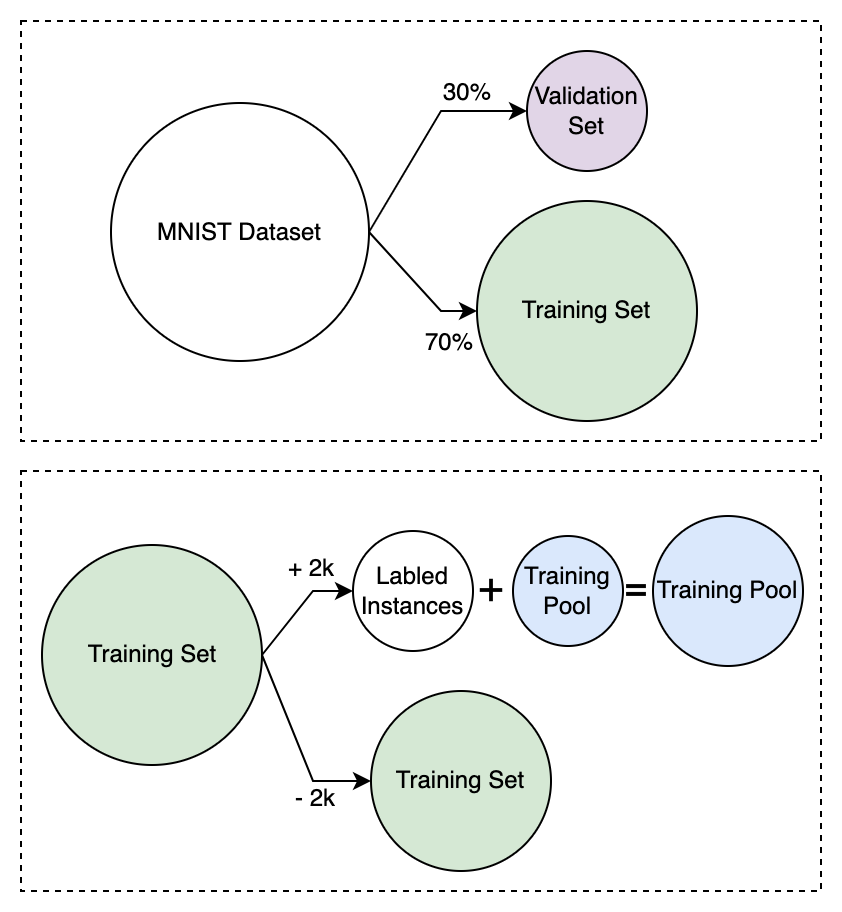
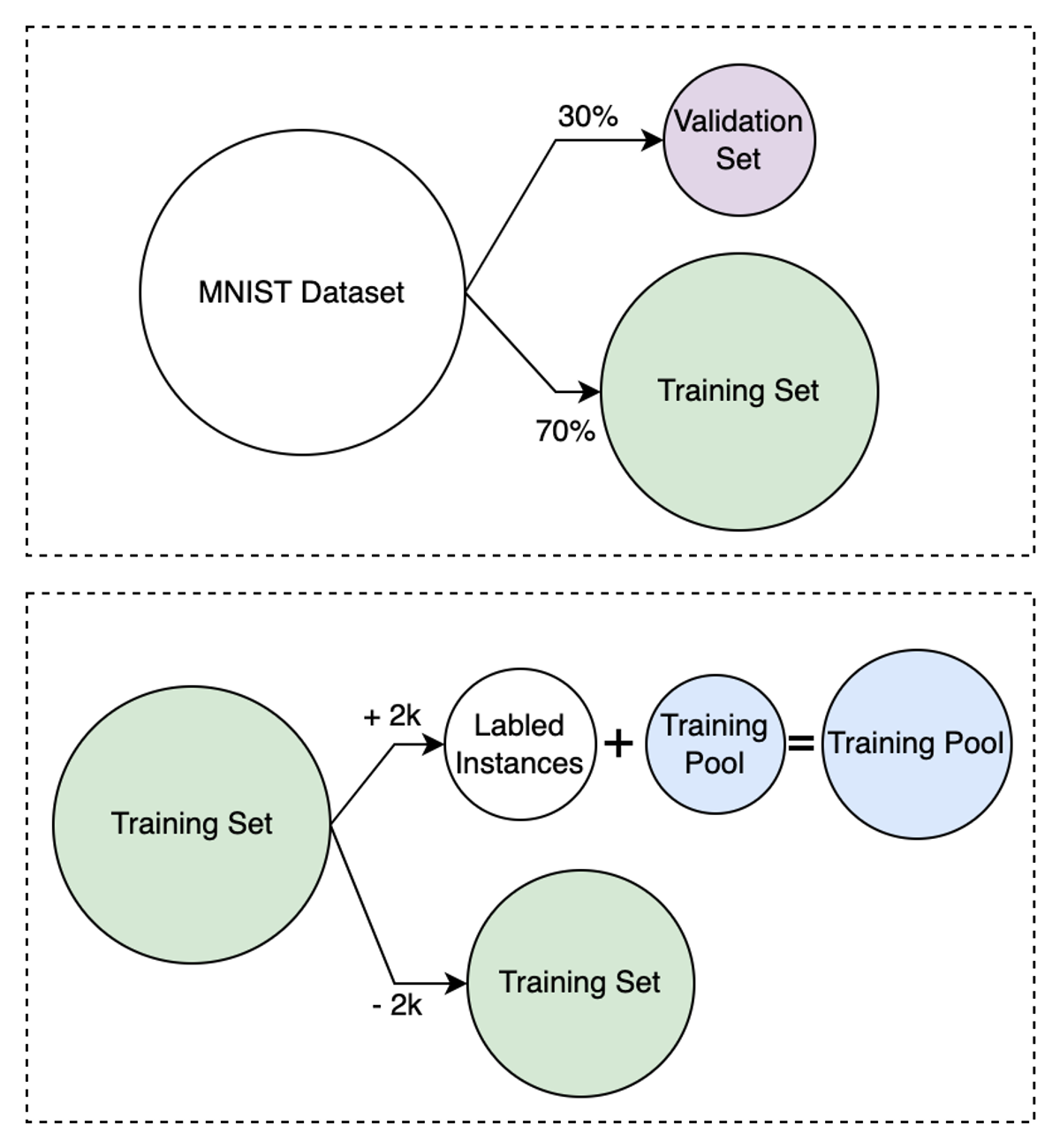
Figur 5: Opprettelse av forskjellige dataset og subset

Figur 5: Opprettelse av forskjellige dataset og subset

I figuren over kan vi se hvordan det originale MNIST datasettet først er delt opp i et treningssett og et valideringssett med en 70/30 fordeling. Deretter ser vi hvordan vi iterativt henter 2000 samples fra treningssettet, labler dem og legger dem til i trenings-“poolen”. Dette er gjort for å simulere den “aktive” delen av aktiv læring. Maskinlæremodellen vår vil til en hver tid bli trent på den nyeste oppdateringen av treningspoolen.

Kodeeksempel

Vi starter med å opprette 2 tomme sett, X_pool og y_pool(Training pool i Figur 5), disse vil holde på dataene og labels vi bruker til å trene modellene våre. Først fyller vi disse med 1000 tilfeldige samples fra X_train (Training Set i Figur 5).

(NB: Hvordan X_train og y_train blir laget vil bli forklart til slutt i artikkelen)

Etter at dette er gjort starter vi selve treningsløkken. Den kjører til vi er tom for data i treningssettet. Inne i løkken lager vi en dyp læremodell for hver gjennomkjøring og trener den på dataene i X_pool og y_pool

Neste steg er å legge til mer data i X_pool og y_pool, klar til neste gjennomkjøring. I kodesnippeten over ser vi at dette gjøres på 2 ulike måter ettersom active_learningflagget er satt til True eller False. Enten hentes det ut data ved å bruke funksjonen pick_n_least_confident_images eller så velges de tilfeldig.

I kodesnutten over ser vi hvordan modellen lages, det er enkelt og greit en 3-lags DNN (Dense Neural Network).

Så må vi jo trene modellen, dette gjøres som vist over. Vi holder oss til en veldig enkel modell med standard hyperparametere.

Uncertainty Measure
Endelig har vi kommet til punktet der vi skal se på den delen av algoritmen som faktisk velger samples til modellen vår. For å kunne prioritere hvilke samples vi velger fra treningssettet til treningspoolen, må vi ha en måte å måle og sammenligne hvor nyttige samples i treningssettet er. Dette gjør vi ved å bruke en såkalt “Uncertainty Measure”, en metode for å måle hvor usikker modellen vår er på en gitt input. Teorien er at de dataene modellen vår føler seg mest usikre på også er de den kan lære mest av i fremtiden.

Eksempler på ulike Uncertainty Measures er:

• Least Confidence Uncertainty
• Smallest Margin Uncertainty
• Largest Margin Uncertainty
• Entropy Reduction

I denne artikkelen bruker vi Least Confidence Uncertainty hovedsakelig fordi den fungerer bra til dette eksempelet og den er relativt grei å forstå.

Least Confidence Uncertainty
For å forklare least confidence uncertainty skal vi ta en kjapp titt på en tegning og en dataframe fra koden vår.

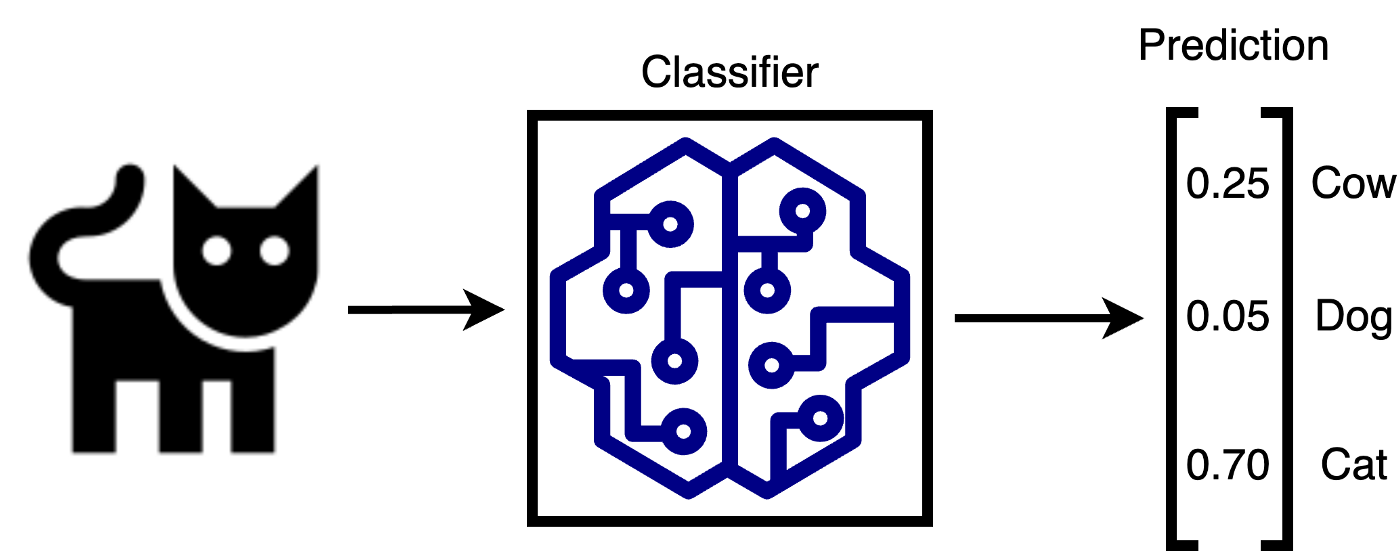
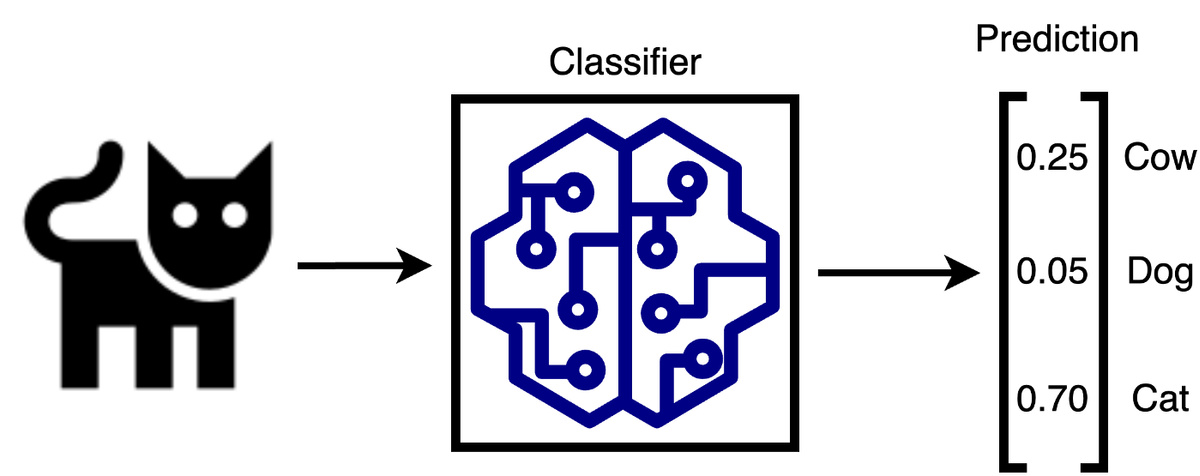
Figur 6: Multiclass classifier

Figur 6: Multiclass classifier

I figuren over ser vi en modell som klassifiserer bilder av dyr samt hvordan outputen fra modellen ser ut. Vi ser at outputen til modellen er en vektor bestående av flyttall, der hvert tall representerer hva modellen tror “sannsynligheten” er for at inputen tilhører de ulike klassene.

I least confidence uncertainty henter vi først ut hva maks verdien er for alle samples i treningssettet, i tilfellet over ville dette vært 0.70. Deretter rangerer vi samplene fra lavest til høyest maks-verdi, der de med lavest maksverdi er de modellen var minst confident på. Det er de samplene med lavest maksverdi som blir valgt ut til merking av mennesker og som vil bli lagt til i treningspoolen for å bli brukt i neste iterasjon av treningsløkken.

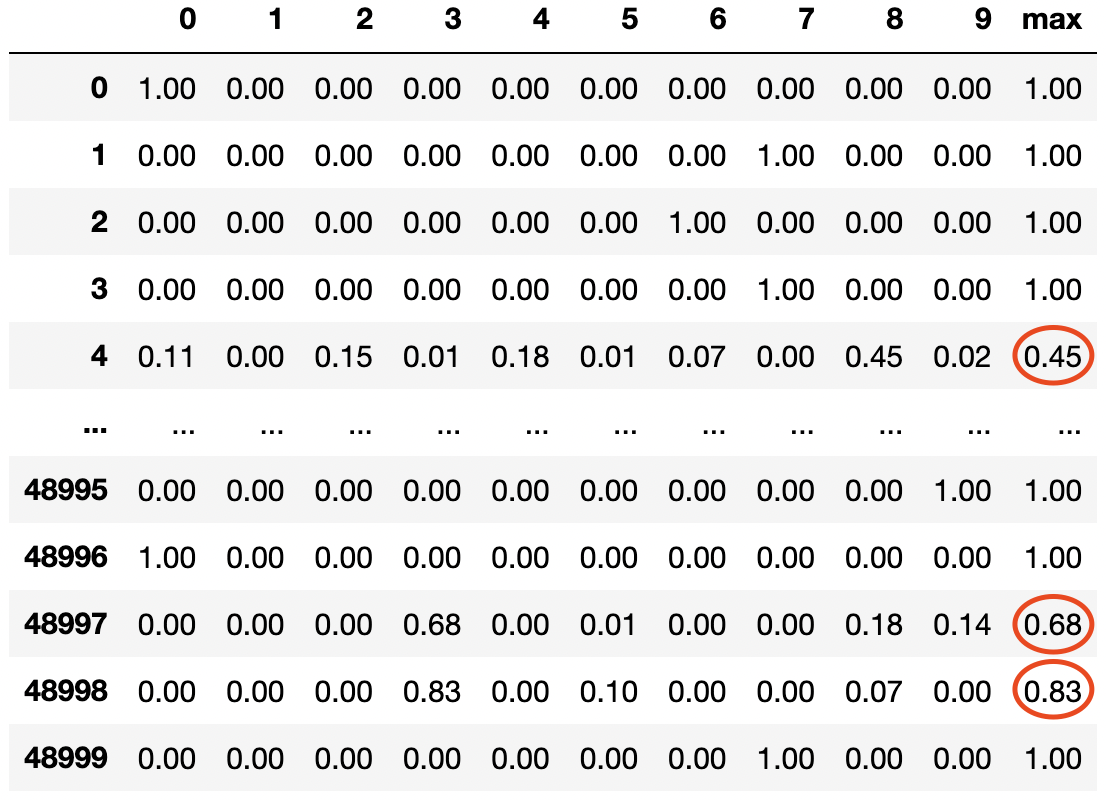
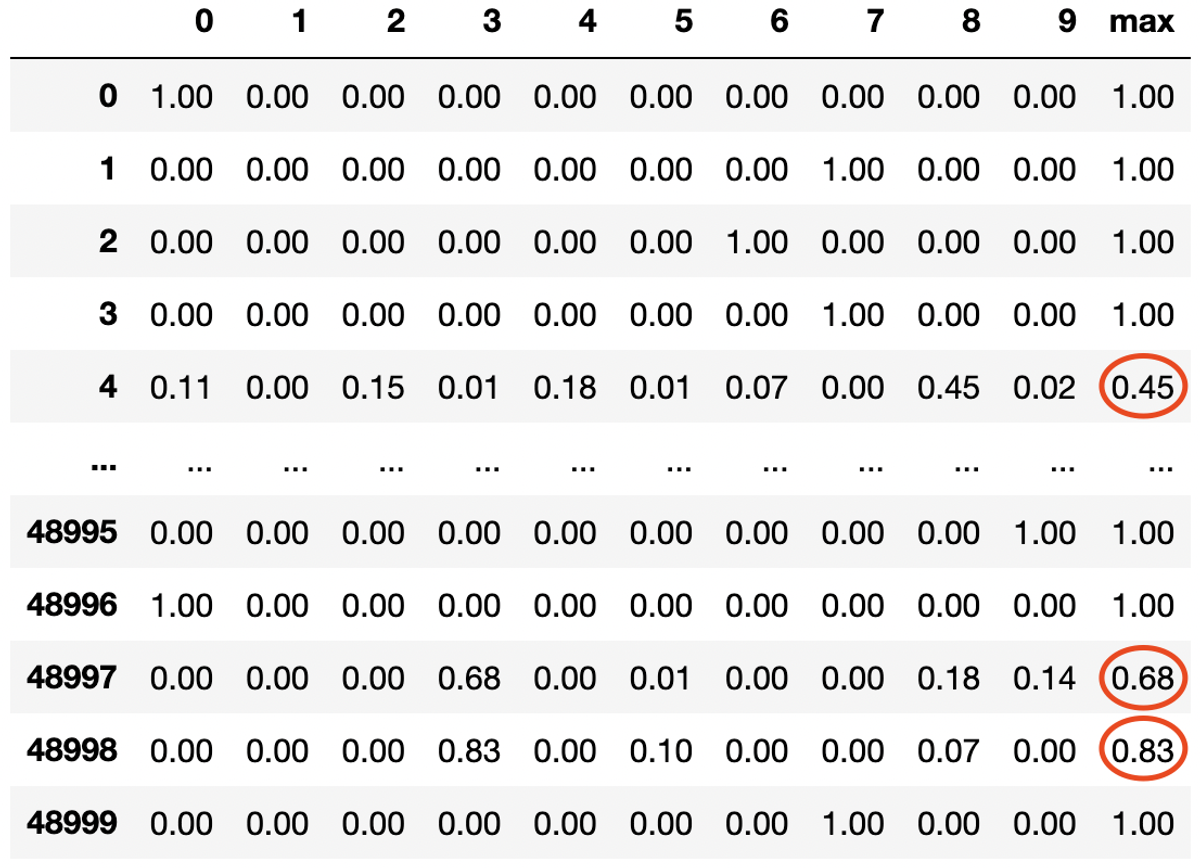
Figur 7: Dataframe med prediksjoner, hver rad er en sample, hver kolonne representerer en klasse

Figur 7: Dataframe med prediksjoner, hver rad er en sample, hver kolonne representerer en klasse

I figuren over ser vi en dataframe med prediksjonene til en modell i kodeeksempelet vårt. Hver rad representerer prediksjonene til modellen for en sample og hver kolonne representerer prediksjonen for en gitt klasse. I figuren over ville de 3 samplene med lavest maksverdi (de som er markert i rødt) vært de mest nyttige for modellen, og det er disse vi burde merke før neste iterasjon av treningsløkken vår.

I kodesnippeten over har vi implementert en veldig enkel versjon av Least Confidence Uncertainty. Stegene i algoritmen er som følger:

1. Gjør en prediksjon på X_train, dataene modellen enda ikke har trent på.
2. Finn den høyeste predikerte verdien for hver sample.
3. Hent indexen til de n samplene med lavest predikert verdi, m.a.o de samplene modellen var mest usikker på.
4. Bruk indexene til å hente ut disse samplene, og lablene fra X_train og y_train. (Dette steget simulerer at et menneske labler samplene)
5. Fjern samplene fra X_train

Resultater

Tidsbesparing?

Vi påstod innledningsvis at den største styrken med aktiv læring er å redusere hvor mye data vi trenger å merke for å oppnå en bra klassifiseringsmodell. Nå skal vi ta en titt på om denne påstanden er sann!

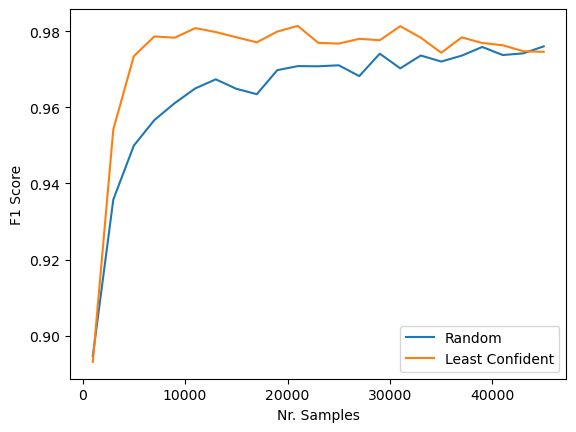
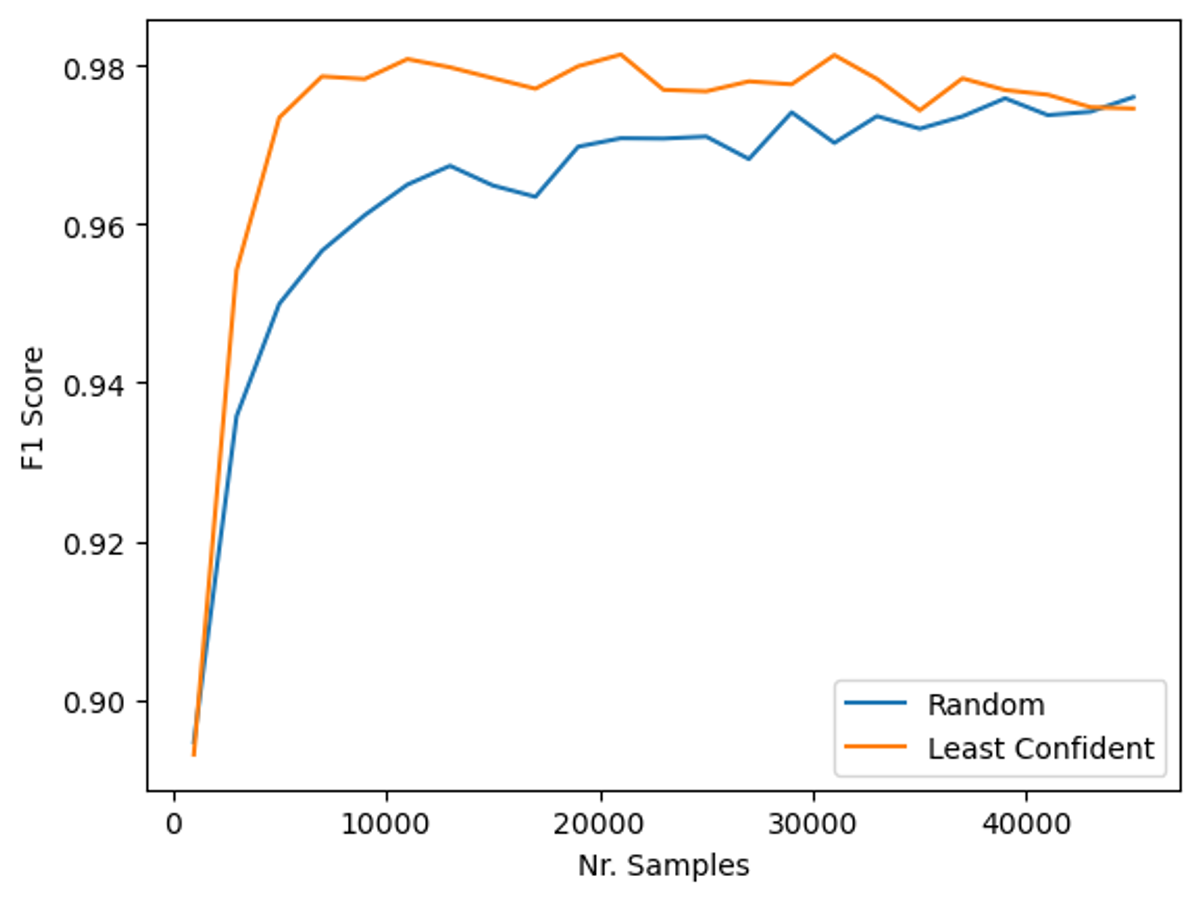
Figur 8: Presisjon over antall samples random vs Least Confident

Figur 8: Presisjon over antall samples random vs Least Confident

I figuren over kan vi se et plott over resultatene over tid ved å kjøre treningsløkken vår. På X-aksen ser vi hvor mange samples vi har i treningspoolen og på Y-aksen ser vi hva nøyaktigheten til modellen er på test-settet.

Man kan tydelig se at modellen som bruker tilfeldig utvelgelse av samples trenger mye mer data før den klarer å nå samme nøyaktighet som modellen trent med least confident uncertainty.

Modellen trent ved least confident uncertainty trengte 6.5 ganger mindre treningsdata! Med andre ord kunne man redusert tiden det tok å merke data med hele 85 %

Visualisering med PCA og t-SNE

Over kunne vi se hvorfor aktiv læring kan være lurt å bruke, i denne seksjonen skal vi se om vi klarer å gjenskape tegningen i figuren under, men med en ekte classifier trent på et ekte multidimensjonelt datasett.

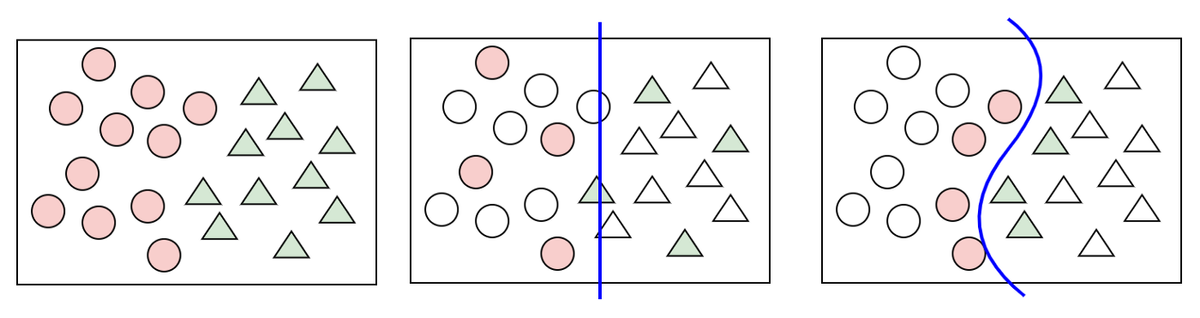
Figur 9: Datasett med 2 klasser (t.v), classifier på random utvalg (midten) og classifier på samples valgt ved å bruke en uncertainty measure (t.h)

Figur 9: Datasett med 2 klasser (t.v), classifier på random utvalg (midten) og classifier på samples valgt ved å bruke en uncertainty measure (t.h)

I figuren over ser vi igjen tegningene fra figur 3, det er disse vi ønsket å gjenskape med ekte data.

Figur 10: Scatterplot av MNIST vha. PCA og t-SNE

Figur 10: Scatterplot av MNIST vha. PCA og t-SNE

Over kan vi se et scatterplot av hele MNIST datasettet oppnådd ved å bruke PCA og t-SNE, tilsvarende plottet til venstre i figur 9.

Figur 11: Scatterplot av MNIST, grå sirkler representerer samples i treningssettet, røde representerer samples i treningspoolen (valgt tilfeldig)

Figur 11: Scatterplot av MNIST, grå sirkler representerer samples i treningssettet, røde representerer samples i treningspoolen (valgt tilfeldig)

I figuren over vises de samme grupperingene av samples. Men i stedet for å fargekode de forskjellige klassene har vi her fargekodet samples som har blitt valgt ut til trening gjennom tilfeldig seleksjon (plot 2 i figur 9).

Figur 12: Scatterplot av MNIST, grå sirkler representerer samples i treningssettet, røde representerer samples i treningspoolen (valgt ved å bruke least confidence uncertainty)

Figur 12: Scatterplot av MNIST, grå sirkler representerer samples i treningssettet, røde representerer samples i treningspoolen (valgt ved å bruke least confidence uncertainty)

I figur 12 viser vi tilsvarende figur, men nå er samples valgt ved å bruke least confidence uncertainty (tilsvarende plot 3 i figur 9).

Som vi kan se i figur 11 er de røde sirklene fordelt jevnt utover alle grupperingene, slik vi ville forventet når vi velger samples tilfeldig. I figur 12 kan vi se at de røde sirklene gjerne er sentrert på “kanten” av grupperingene i overgangen til andre grupperinger. Dette er samples som ligner på flere klasser i datasettet, som er vanskelig å gjenkjenne og som modellen vår kan lære mye av ☺️

Treningsoppsett

Denne seksjonen inneholder ikke noe spesifikt for aktiv læring, men gir en rask forklaring av resten av koden i notebooken.

Først bruker vi sklearn sin fetch_openml funksjon for å laste MNIST datasettet inn i minnet. Deretter henter vi ut bildene og labels i hver sine variabler. Til slutt normaliserer vi verdiene i bildene til en verdi mellom 0 og 1.

Deretter deler vi MNIST opp i trenings- og valideringsset og shuffler bildene.

NB! Legg merke til av vi bruker random_state, dette gir oss den samme tilfeldige fordelingen av trenings- og valideringssett og shufflingen av bildene for hver gang. Da er vi sikre på at modellene vi trener ikke har noen fordeler/ulemper når det gjelder dataene de trenes på.

Potensielle forbedringer og videre arbeid

I denne artikkelen har vi kun fokusert på en form for Uncertainty Measures, nemlig Least Confidence Measure. Det er ikke sikkert at dette er den optimale måten å velge samples på, kanskje kunne en av de andre metodene nevnt under seksjonen Uncertainty Measures gitt bedre resultater?

Vi har også valgt å lage et DNN (Dense Neural Network) som modell for å klassifisere bilder. Dette er ikke den best egnede formen for maskinlære- modell for dette problemet og man vil nok fått andre resultater om man hadde f.eks brukt en CNN (Convolutional Neural Network). Om dette ville hatt en innvirkning på tidsforbruket er derimot usikkert, kanskje modellen hadde klart å oppnå en høyere nøyaktighet enda raskere enn den som ble laget i dette eksperimentet?

Avslutningsvis er det verdt å nevne at vi implementerte Uncertainty Measurement-algoritmen selv i denne artikkelen, heldigvis trenger man ikke gjøre dette hver gang. Biblioteker som modAL kan være med på å gjøre aktiv læring prosessen vesentlig mye enklere.

Referanser

[1]: https://www.openml.org/search?type=data&sort=runs&id=554&status=active

[2]: https://en.wikipedia.org/wiki/Principal_component_analysis

[3]: https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding